太极图形60行代码实现经典论文，0.7秒搞定泊松盘采样，比Numpy实现快100倍

萧箫 2022-06-15 21:23:05 来源：量子位

编辑整理自 太极图形
量子位 | 公众号 QbitAI

由随机均匀的点组成的图案，在动植物身上已经很常见了。

像杨梅、草莓、荔枝、红毛丹这样的水果，表面都有颗粒或者毛发状的结构，它们随机、均匀地散布在水果表面：

类似的图案在动物身上也有，比如大家都爱涮的毛肚：

同样地，在计算机模拟下，也有不少场景需要在空间中随机、均匀地生成点。

像生成动物毛发时的毛孔位置、多人对战游戏中的玩家出生位置、生成森林时的树木位置等等。

这些场景的共同特点是，都需要让任何两点之间的距离大于等于一个下界（这个下界是预设的，改变它就可以控制生成点之间的间隔）。

但如果直接使用完全随机生成的点，大概率会获得一个很不均匀的分布结果，有些地方“扎堆”、有些地方稀疏：

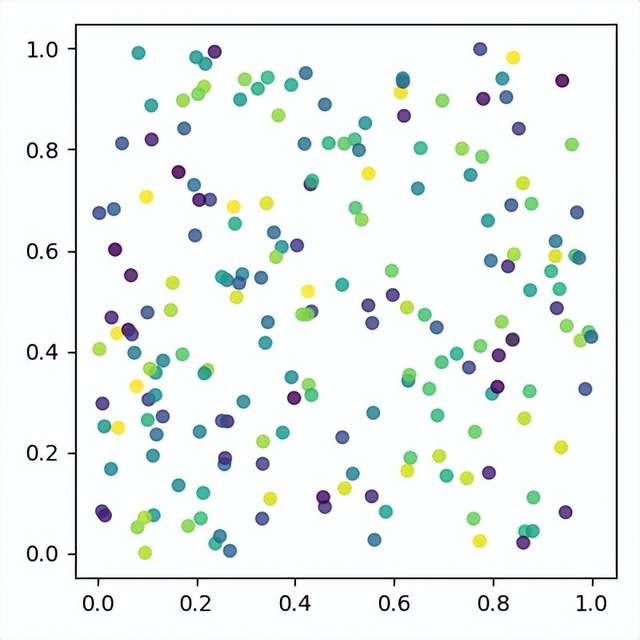
如果用这样的点来模拟毛发等位置生成，效果就很差。

所以，需要在生成点的过程中加入一个距离判断，来剔除那些不合要求的点。

此前，用NumPy生成这样一个效果，往往需要70s左右，非常不划算。

现在，太极图形基于Taichi实现了一个超快算法，同样的效果运行在单个CPU线程上，只需要0.7s就能生成这样的图案，快了100倍左右。

一起来看看他们是怎么做的。

采用Bridson算法实现

此前，有一种常见算法是dart throwing （像一个人蒙上眼睛胡乱扔飞镖的样子）：

每次在区域内随机选择一个点，并检查该点与所有已经得到的点之间是否存在“冲突”。

若该点与某个已得到的点的最小距离小于指定的下界，就抛弃这个点，否则这就是一个合格的点，把它加入已有点的集合。

重复这个操作直到获得了足够多的点，或者连续失败了N次为止（N是某个设定的正整数）。

但这种算法的效率很低。

因为随着得到的点的个数增加，冲突的概率越来越大，获得新的点所需的时间也越来越长，每次比较当前点和所有已有点之间的距离也会降低效率。

相比之下，Bridson算法则要更加高效。

这个算法的原理来自于Robert Bridson发表于2007年的论文”Fast Poisson Disk Sampling in Arbitrary Dimensions”[1]（论文非常短，只有一页A4纸），如果再去掉标题、引言的话，真正的算法内容只有一小段话。

开头这个动图，演示了Bridson圆盘采样算法在一个400×400的网格区域上的运行效果，算法尝试获得100K个均匀散布的点，实际生成了大约53.7K个：

这个动画是使用Taichi生成的，运行在单个CPU线程上，除去编译的时间计算，耗时仅在0.7s多一点，而同样的代码翻译成NumPy要耗时70s左右。[2]

从上面的动画效果可见，Bridson算法很像包菜的生长过程：我们从一个种子点开始，一层一层地向外添加新的点。

每一次我们添加的新的点，都位于最外层的点的周围，并且尽可能地包住最外层。

为了避免每次都检查和所有已有点之间的距离，Taichi采用了所谓网格化的技巧：

将整个空间划分为网格，对一个需要检查的点，只要找到它所在的网格，然后检查它和临近网格中的点之间的最小距离即可。

只要这个距离大于指定的下界，更远处的点就不必再检查了。这个技巧在图形学和物理仿真中是非常常用的。

这个采样过程很难并行化，因为当一个线程“偷偷”加入一个新的点的时候，会改变其它所有线程对距离的判断。所以Taichi仅使用单个CPU线程来执行这个算法：

ti.init(arch=ti.cpu)

上面的代码中通过指定arch=ti.cpu来让程序运行在CPU上。

你可能会想，既然是单线程+CPU，那为什么不直接写纯Python呢？别着急，我们的计算部分会放在ti.kernel函数中，这种函数并不运行在Python虚拟机中，而是会被Taichi编译执行，所以会比纯Python的实现快很多倍！

在我们介绍Bridson算法的具体实现之前，你不妨猜猜这个Taichi程序包含多少行代码？

安装和导入Taichi

首先推荐大家使用最新的Taichi发布版本，这样可以使用更丰富的功能，在不同平台上的支持也更稳定。截止本文写作时最新版本是1.0.3:

pip install taichi==1.0.3

然后，在代码开头写上：

import taichi as ti
import taichi.math as tm

这样会导入Taichi以及Taichi的math模块。math模块除了包含常用的数学函数之外，还提供了非常方便的向量运算。

准备工作

在泊松采样算法中，采样点之间的距离有一个下界r。

我们假设整个区域是由N×N个同样大小的方格组成的网格区域，使得每个小方格的对角线长度正好是r，即网格的边长是r/√2。

于是任何小方格中至多包含一个点。如下图所示：

这就是我们前面提到的网格化方法，即对于任何一个点p，设它所在的方格是D，则任何与p的距离小于等于r的点必然位于以D中心的、由5×5个方格组成的正方形区域中。

在检查距离时，我们只要针对这个子区域进行计算即可。

我们用一个一维数组samples和一个N×N的二维数组grid来记录已经得到的采样点：

1. samples保存当前所有已经采样点的坐标，它的每个元素是一个二维坐标（x,y）。
2. grid[i, j]是一个整数，它存储的是第（i, j）个方格中采样点在数组samples中的下标。grid[i, j] = -1表示这个方格中没有采样点。

于是我们的初始设置可以这样写：

grid_n = 400
res = (grid_n, grid_n)
dx = 1 / res[0]
inv_dx = res[0]
radius = dx * ti.sqrt(2)
desired_samples = 100000
grid = ti.field(dtype=int, shape=res)
samples = ti.Vector.field(2, float, shape=desired_samples)

这里网格大小设置为400×400，它占据的平面区域是[0,1]×[0,1]，所以网格的步长是dx = 1/400。采样的最小间隔是每个小方格对角线的长度，即radius = sqrt(2)*dx。

我们把采样点的目标个数设置为desired_examples=100000，这是一个目测值，因为400×400的网格包含160000个小方格，考虑到每个方格中至多只有一个点，我们能得到的满足距离约束的点的最大数目肯定少于160000。

初始时网格中没有任何点，所以需要将grid中的值都置为-1:

grid.fill(-1)

如何生成新的点

在加入新的随机点时，我们总是从已有点的附近随机选择一个位置，然后比较它和已知点是否满足最小距离约束，是的话就将其加入已有点，否则就将其抛弃然后重新选择点。

这里需要注意的是：

1. 当一个已有点附近已经被填满时，我们后面再加入新的点时就不必考虑它的附近了，可以用一个下标head来记录这一点。我们约定samples数组中下标< head的点附近都已经被填满，从而不必再考虑它们，只考虑下标>= head的点即可。初始时head = 0。
2. samples是一个长度为100K的数组，这不代表我们真的能取到这么多点，但具体个数是多少无法事先确定，所以我们还需要用一个下标tail来记录目前已经获得的点的个数。初始时tail = 1，因为我们将选择区域中心作为第一个点。当然这个初始点的位置可以是任意的。
3. 正如前面提到的，当我们检查一个点p是否与已有点满足最小距离约束时，没有必要遍历检查所有的点。只要检查以p所在方格为中心，由5×5个方格组成的正方形区域即可。

检查一个点是否和已有点冲突的逻辑我们单独写成一个函数：

@ti.func
def check_collision(p, index):
    x, y = index
    collision = False
    for i in range(max(0, x - 2), min(grid_n, x + 3)):
        for j in range(max(0, y - 2), min(grid_n, y + 3)):
            if grid[i, j] != -1:
                q = samples[grid[i, j]]
                if (q - p).norm() < radius - 1e-6:
                    collision = True
    return collision

其中p是需要检查点的坐标，index=(x, y)是p所在的方格的下标。

我们遍历所有满足x-2 <= i <= x+2和y-2 <= j <= y+2的下标(i, j)，检查方格(i, j)中是否已经有点，即 grid[i, j]是否等于-1。有的话它与p的距离是否小于radius，然后返回对应的判断。

完成了准备工作，我们可以开始正式的循环了：

@ti.kernel
def poisson_disk_sample(desired_samples: int) -> int:
    samples[0] = tm.vec2(0.5)
    grid[int(grid_n * 0.5), int(grid_n * 0.5)] = 0
    head, tail = 0, 1
    while head < tail and head < desired_samples:
        source_x = samples[head]
        head += 1

        for _ in range(100):
            theta = ti.random() * 2 * tm.pi
            offset = tm.vec2(tm.cos(theta), tm.sin(theta)) * (1 + ti.random()) * radius
            new_x = source_x + offset
            new_index = int(new_x * inv_dx)

            if 0 <= new_x[0] < 1 and 0 <= new_x[1] < 1:
                collision = check_collision(new_x, new_index)
                if not collision and tail < desired_samples:
                    samples[tail] = new_x
                    grid[new_index] = tail
                    tail += 1
    return tail

首先我们把区域的中心，即坐标为(0.5,0.5)的点选择为初始点，让它作为“种子”将随机点逐渐扩散到整个区域。

接下来的while循环是算法的主体，这个循环是串行执行的，只占用一个线程。

我们每次找到第一个需要考虑的点samples[head]，然后在以它为中心，半径为[radius, 2*raidus]的圆环中随机选择100个点，逐个检查这100个点是否不超出[0,1]×[0,1]的区域范围，以及是否和已有点冲突。

如果都满足的话它就是一个合格的点，我们将它的坐标和方格下标更新到samples和grid中，并将已有点的个数tail增加1。在这100个点都检查完后，可能有多个点会被加入已有点的集合。

注意在半径为[radius, 2*raidus]的圆环中采样可以让我们得到的点在满足最小距离约束的同时距离已有点也不会太远。

当这100个点都检查完毕后，我们可以认为samples[head]这个点的周围已经没有空白区域可以放置新的点，所以将head增加1，并重新检查下一个samples[head] 附近的区域。

当所有的点周围的空间都已经被填满，即head = tail时，或者我们已经获得了desired_samples个点，即tail = desired_samples时循环结束。这时samples中下标在0~tail-1范围内的点就是全部的已有点。

展示动画效果

我们可以只用几行代码，就把整个采样的过程用动画的形式显示出来：

num_samples = poisson_disk_sample(desired_samples)
gui = ti.GUI("Poisson Disk Sampling", res=800, background_color=0xFFFFFF)
count = 0
speed = 300
while gui.running:
    gui.circles(samples.to_numpy()[:min(count * speed, num_samples)],
                color=0x000000,
                radius=1.5)
    count += 1
    gui.show()

这里我们控制动画的速度为每生成300个点就绘制一帧。

至此我们已经介绍完了程序的所有要点，把各部分组合起来：

import taichi as ti
import taichi.math as tm
ti.init(arch=ti.cpu)

grid_n = 400
res = (grid_n, grid_n)
dx = 1 / res[0]
inv_dx = res[0]
radius = dx * ti.sqrt(2)
desired_samples = 100000
grid = ti.field(dtype=int, shape=res)
samples = ti.Vector.field(2, float, shape=desired_samples)

grid.fill(-1)

@ti.func
def check_collision(p, index):
    x, y = index
    collision = False
    for i in range(max(0, x - 2), min(grid_n, x + 3)):
        for j in range(max(0, y - 2), min(grid_n, y + 3)):
            if grid[i, j] != -1:
                q = samples[grid[i, j]]
                if (q - p).norm() < radius - 1e-6:
                    collision = True
    return collision

@ti.kernel
def poisson_disk_sample(desired_samples: int) -> int:
    samples[0] = tm.vec2(0.5)
    grid[int(grid_n * 0.5), int(grid_n * 0.5)] = 0
    head, tail = 0, 1
    while head < tail and head < desired_samples:
        source_x = samples[head]
        head += 1

        for _ in range(100):
            theta = ti.random() * 2 * tm.pi
            offset = tm.vec2(tm.cos(theta), tm.sin(theta)) * (1 + ti.random()) * radius
            new_x = source_x + offset
            new_index = int(new_x * inv_dx)

            if 0 <= new_x[0] < 1 and 0 <= new_x[1] < 1:
                collision = check_collision(new_x, new_index)
                if not collision and tail < desired_samples:
                    samples[tail] = new_x
                    grid[new_index] = tail
                    tail += 1
    return tail

num_samples = poisson_disk_sample(desired_samples)
gui = ti.GUI("Poisson Disk Sampling", res=800, background_color=0xFFFFFF)
count = 0
speed = 300
while gui.running:
    gui.circles(samples.to_numpy()[:min(count * speed, num_samples)],
                color=0x000000,
                radius=1.5)
    count += 1
    gui.show()

代码总行数：60。

One More Thing

具体来说，这篇代码实现了两个操作：

1. 在60行代码中实现了一个完整的泊松采样动画。
2. 在一个400×400的网格中采集了53k个点，但耗时不到1秒。

相关代码可以在文末的原文链接中找到。

严格来说，本文实现的算法和Bridson论文里描述的算法有一点点不一样的地方（更简单一些），但是效果却差不多。

你能看出是哪里不一样吗？（TIP：可以关注一下原论文Step 2中“active list”的处理方式）

项目地址：
https://github.com/taichi-dev/poisson-sampling-homework

参考资料：
[1]Robert Bridson的原论文见Fast Poisson Disk Sampling in Arbitrary Dimensions.
[2]Poisson采样用Taichi, Numpy, Numba实现的benchmark比较见GitHub