矩阵乘法计算速度再次突破极限，我炼丹能更快了吗？| 哈佛、MIT
O(n^2.3728596)
梦晨 发自 凹非寺
量子位 报道 | 公众号 QbitAI
n阶矩阵乘法最优解的时间复杂度再次被突破，达到了O(n^2.3728596)。
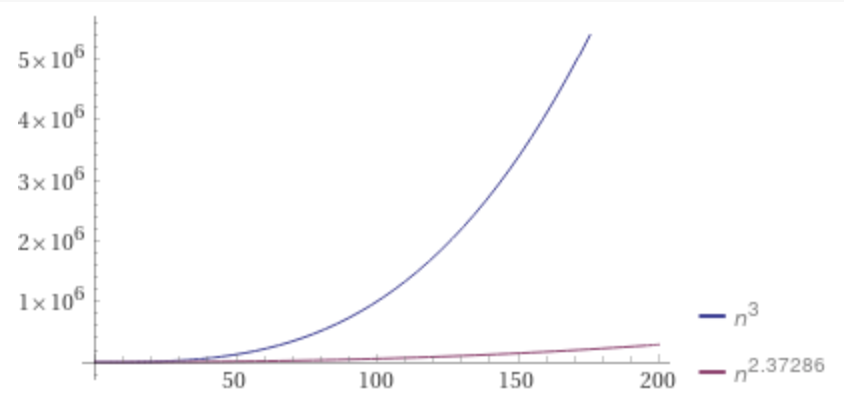
按定义直接算的话，时间复杂度是O(n³)。
光这么说可能不太直观，从图上可以看出，n足够大时优化后的算法就开始表现出明显优势。
矩阵乘法在深度学习中有着广泛的应用，像卷积神经网络(CNN)中最耗时间的卷积计算，就经常被映射成矩阵乘法。
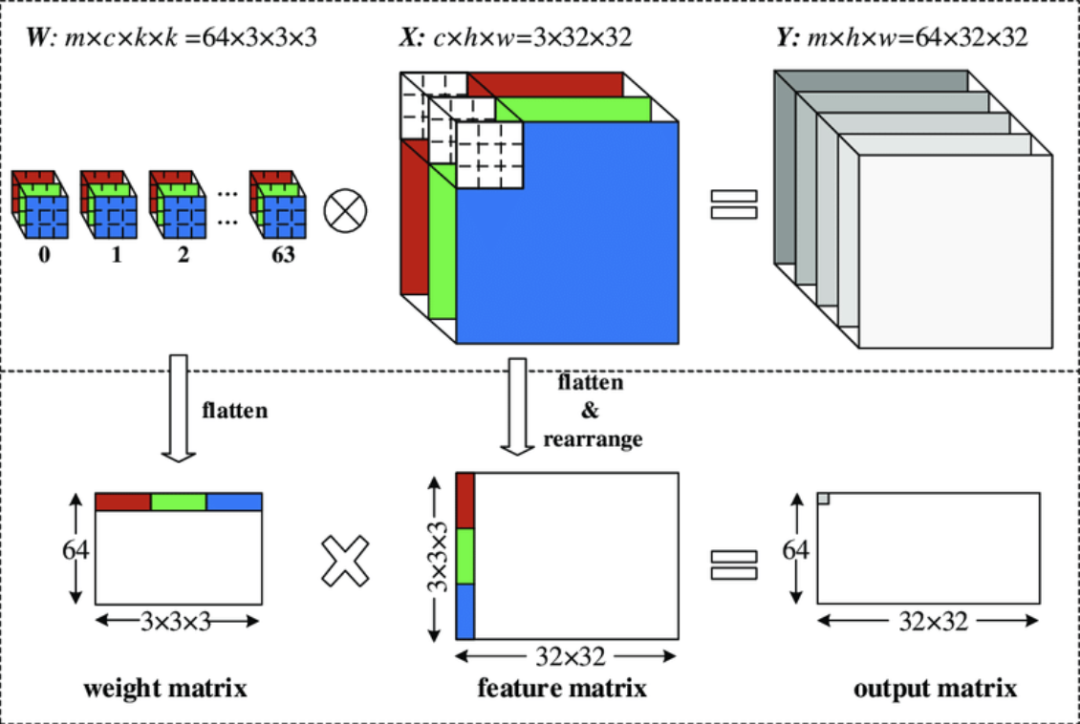
△图源：DOI 10.3390/electronics8010065
虽然在具体实现上还有很多障碍，但矩阵相乘底层算法的优化，至少在理论上为深度学习节省时间提供了可能性。
而科学家们努力的目标，是使n阶矩阵乘法的时间复杂度尽可能接近理论上的最快速度O(n²)。
本次研究共同作者是一对师徒。
△左：Alman 右：Vassilevska Williams
Josh Alman目前是哈佛大学的博士后研究员，主要研究方向是算法设计和复杂度理论。
Virginia Vassilevska Williams是他在MIT读博士期间的导师，研究方向是组合数学和图论在计算领域的应用。
Strassen：用加法替代乘法
矩阵乘法的时间复杂度直到1969年才第一次被Volker Strassen降至O(n³)以下。
看过《算法导论》的同学应该很熟悉Strassen算法。
以2阶矩阵相乘为例，总共需要进行2³=8次乘法，而2ⁿ的高阶矩阵相乘可以用分块法不断迭代细分解成若干个2阶子矩阵相乘。
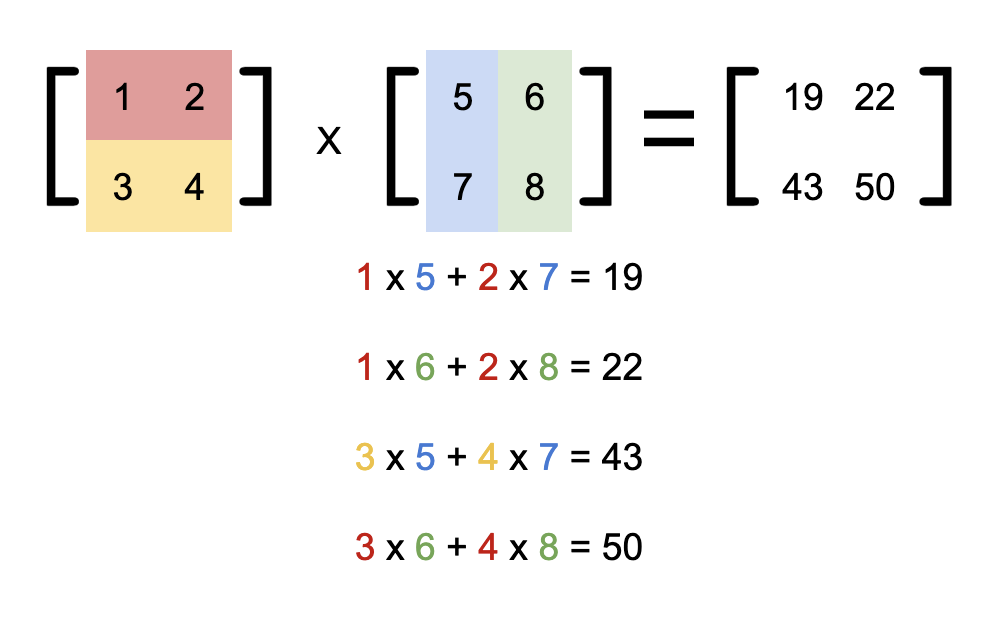
Strassen巧妙地通过构造7个中间变量，用增加14次加法为代价省去了一次乘法。
对于
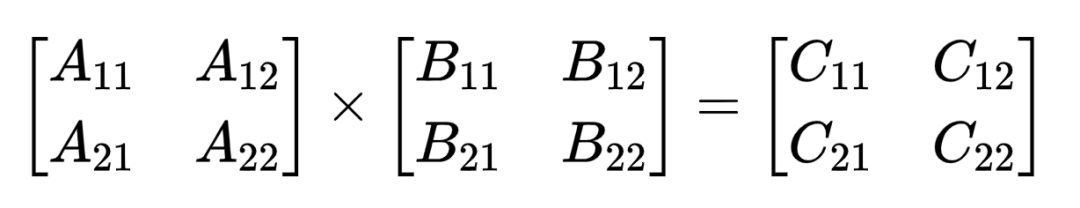
定义
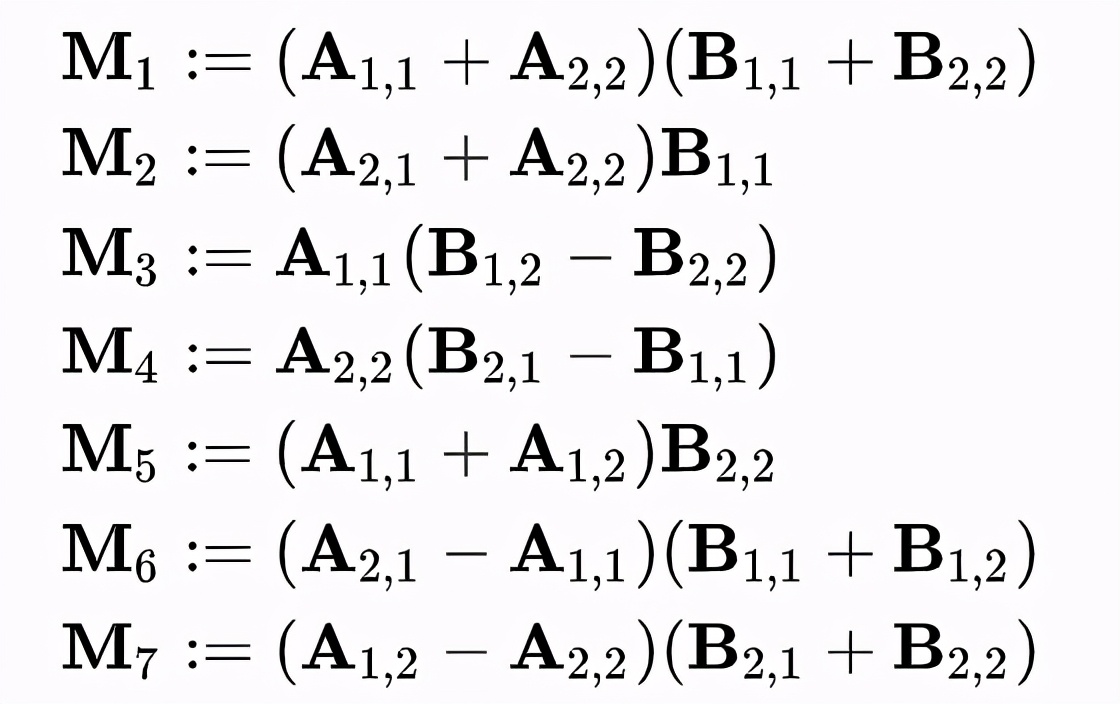
则有
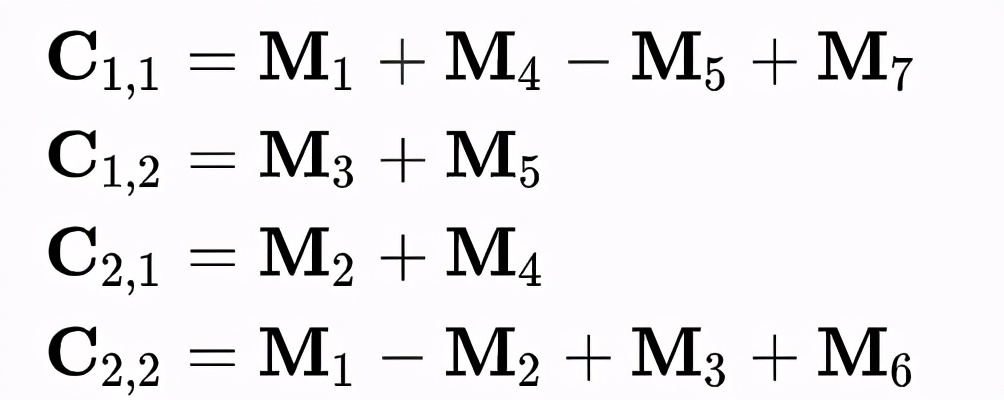
像这样，在M₁-M₇的计算中只有7次乘法操作。由于矩阵乘法计算中乘法的复杂度是O(n³)，而加法的复杂度只有O(n²)，n越大时此方法的收益就越大。
且分块后每个子矩阵相乘都可以省去一次乘法操作，最终把时间复杂度降低到O(n^2.807)。
这么绕的算法到底怎么想出来的？可惜Strassen在论文中并没有说明这一点。
Strassen算法在实际应用时受到很大限制，如运行时会创建大量的临时变量，在n不够大时反倒更耗费时间。
还有只适用于稠密矩阵，针对稀疏矩阵有更快的专门算法。
但最重要的是，Strassen的办法让学界意识到，原来矩阵乘法问题还有优化空间啊！
激光法：用张量替代矩阵
20世纪70年代末期,科学家们找到了解决问题的新思路，将矩阵计算转换为张量计算。
1981年，Schonhage将此方法优化到O(n^2.522)后，Strassen把这个方法命名为“激光法(Laser Method)”，因为和正交偏振激光有相似之处。
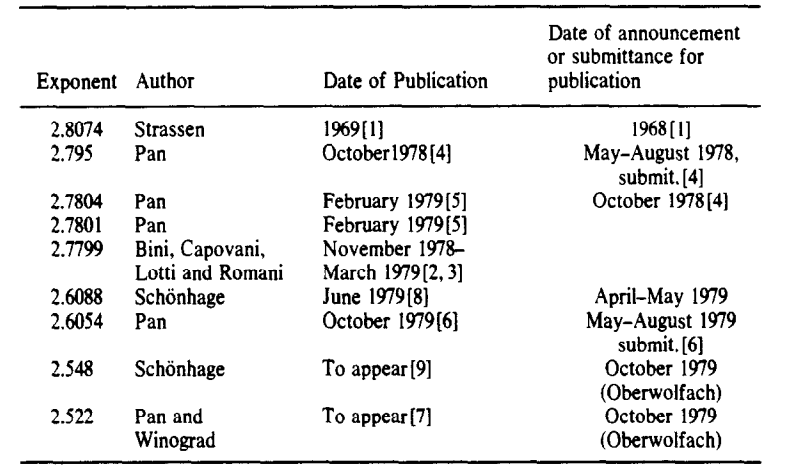
在后来的几十年中，矩阵乘法的每次优化都来自激光法的优化，即如何更有效地把矩阵问题转换成张量问题。
Alman和Williams的优化算法只比14年LeGall的O(n^2.3728639)减少了4e^(-6)。
从历次优化的幅度来看，似乎已逼近激光法的极限。
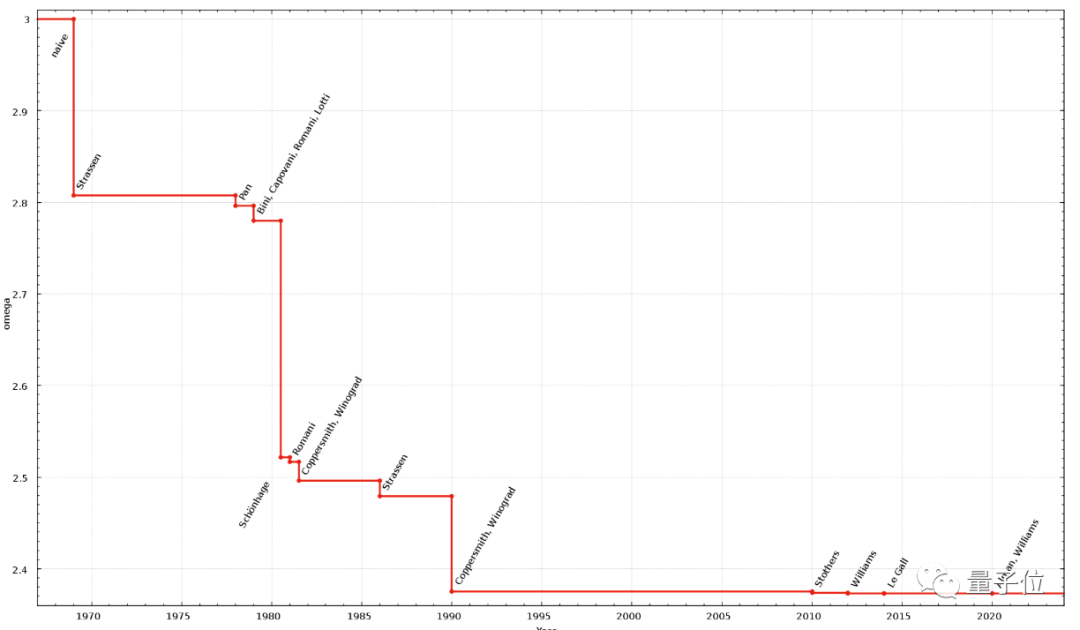
能算得更快了吗？
激光法很少在实际中应用，因为它只在n足够大，大到现代计算机硬件几乎无法处理的时候才能提供优势。
这样的算法被称作“银河算法(Galatic Algorithm)”。
在业界使用最多的还是通过分块法和并行处理控制矩阵的规模。当n不大时，再通过循环展开，内存布局优化等办法针对直觉算法的优化。
还有一点，现实中由于浮点数精度的限制，Strassen法和激光法在计算大规模矩阵时都会产生不小的误差。
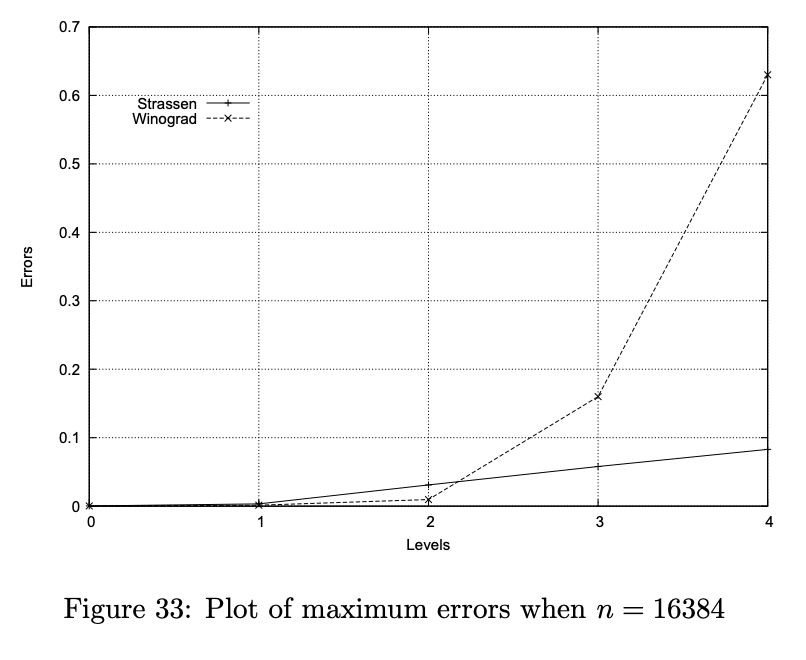
△图源：DOI 10.1109/ICPADS.2011.130
矩阵乘法的加速，看来还没那么容易。
论文链接
https://arxiv.org/abs/2010.05846
参考链接：
[1]https://www.quantamagazine.org/mathematicians-inch-closer-to-matrix-multiplication-goal-20210323
[2]https://en.wikipedia.org/wiki/Matrix_multiplication_algorithm
[3]https://www.researchgate.net/publication/330315719_A_Uniform_Architecture_Design_for_Accelerating_2D_and_3D_CNNs_on_FPGAs
[4]http://www.theoryofcomputing.org/articles/gs005/gs005.pdf
[5]https://www.youtube.com/watch?v=J5LK1SChxGs
[6]http://www.cs.toronto.edu/~yuvalf/AmbFilLeG14.pdf
- 开源Llama版o1来了，3B小模型反超80B，逆向工程复现OpenAI新Scaling Law2024-12-17
- AI音乐战火升级！三路国产大军全面对决Suno2024-12-11
- o1满血版最鲜测！这¥1500花得值吗？2024-12-06
- 谷歌邀马斯克联手做AI游戏！DeepMind版Sora是个3D游戏引擎 profile-avatar2024-12-05
相关阅读
