推荐场景Scaling Law来了!中科大&华为诺亚方舟联合推出
提出推荐大模型性能预测定律
当Scaling Law应用于推荐场景,模型又将如何表现?
中科大认知智能全国重点实验室陈恩红团队联合华为诺亚方舟实验室推出推荐模型性能定律,首次对模型的性能与模型、数据的规模和质量进行了定量分析。

针对现有工作只能对推荐大模型Scaling Law(扩展定律)做定性分析的局限性,论文首次尝试对推荐大模型性能扩展定律给出明确的定量预测。
具体地,相较于传统大模型扩展定律里的数据量指标,考虑推荐领域的数据特性提出了序列数据的质量衡量指标,并从模型性能预测角度出发避免传统扩展定律带来参数增大导致的模型过拟合问题。
最终基于论文发现的推荐大模型性能预测定律,能够在给定的数据集和模型配置下,有效预测模型的扩展潜力,同时实现模型参数的最优性能配置。
下面具体来看。
提出推荐大模型性能预测定律
序列推荐系统旨在根据用户过去的交互记录预测下一个推荐给用户的物品,以此来捕捉用户的动态偏好。
近年来,随着商业和互联网场景中用户数据量的急剧增长,推荐系统受到了越来越多的关注。然而,为了处理这些庞大的数据集,商用与学术领域均开始采用更为复杂和庞大的推荐模型。
这些模型的高计算要求不仅带来了巨大的开发成本,而且还使得开发过程中的资源分配和GPU使用变得充满挑战。
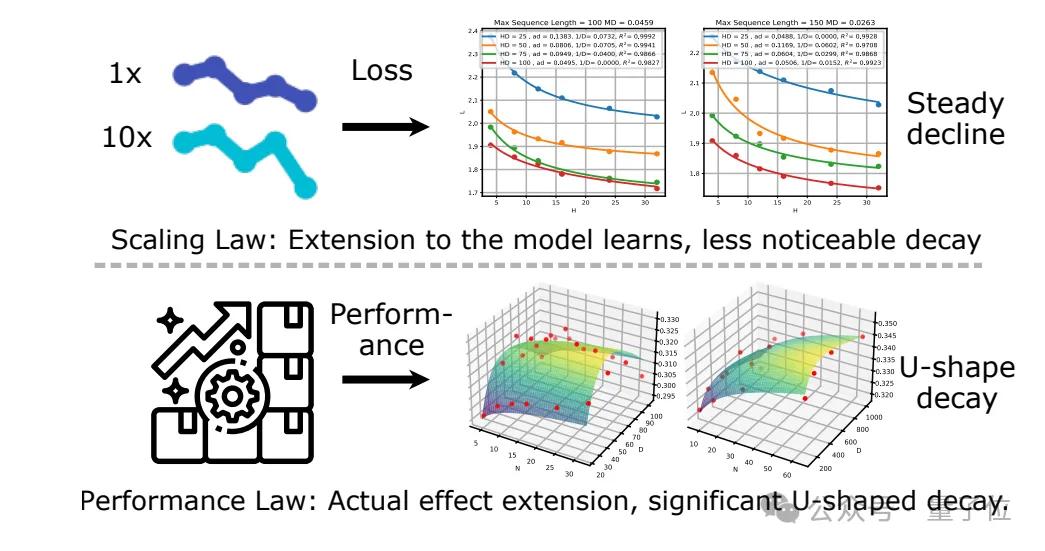
如上图所示,为了更好地预测推荐模型在不同情况下的性能,研究者们开发了一系列的扩展定律,用于在无需进行大规模实验的情况下评估和预测模型效果。
扩展定律最初在大型语言模型中进行探索。例如Chinchilla扩展定律的通过模型参数数量和训练样本的数量来预测预训练损失。
然而,将扩展定律应用于推荐系统分析面临两大主要挑战:
(1) 与扩展定律中通常考察的模型损失指标相比,推荐模型中性能指标(如命中率)更为重要,由扩展定律导向的增大模型规模虽然能使模型损失降低,却会由于模型过拟合问题导致性能出现衰减。
(2) 除了数据的规模之外,推荐系统的数据集通常具有结构和协作特性,同时重复序列片段和冗余度较高,这使得数据质量成为影响结果的核心因素,但在现有的推荐模型扩展定律中尚未被充分讨论。
这些挑战使得现有的推荐系统扩展定律工作仅仅给出了一些定性的分析,并不能对模型的精度进行定量预测。
为应对这些挑战,研究人员提出了推荐大模型性能预测定律,首次对模型的性能与模型、数据的规模和质量进行了定量分析。
通过拟合推荐模型的关键性能指标,包括命中率(HR)和归一化折扣累积增益(NDCG),可以定量预测模型的层数和物品嵌入维度对其性能的影响。
此外,为了应对数据质量研究因素匮乏的挑战,引入了近似熵(ApEn)作为评价数据质量的创新性指标,将原有扩展定律中的数据规模替换为数据规模与近似熵之比,并通过理论和实验验证了这一替代的合理性。
研究人员也对提出的大模型性能预测定律进行了应用实验,有效地预测了模型的最优性能参数配置和扩展潜力。
引入近似熵因子
如前所述,研究人员引入了近似熵因子,以进一步增强序列推荐系统中的扩展定律。
具体来说,近似熵是一种用于量化时间序列数据的规律性和不可预测性的统计测度,其计算方法如下:
首先,对于一个长度为N的时间序列{ }以及参数m(嵌入维度)和r(容差),构造m维向量=[,+1,…,+m-1 ] ,其中=1,…,N-m+1 。然后,定义两个向量和之间的距离为:
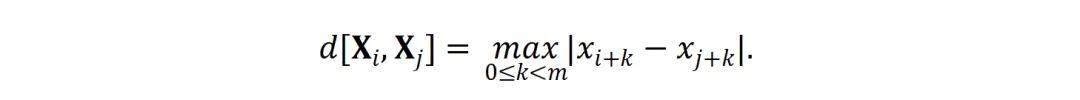
接着,对于给定的容差r ,计算相似性度量:
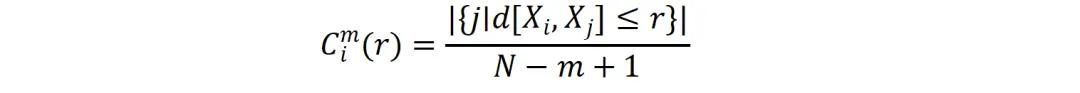
平均相似性的计算公式为:
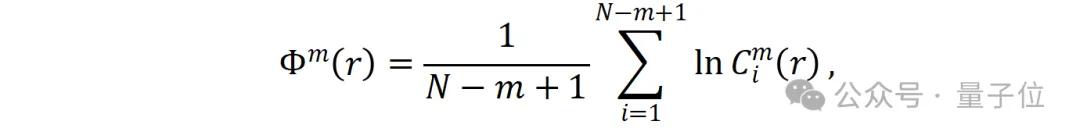
最终,近似熵定义为:
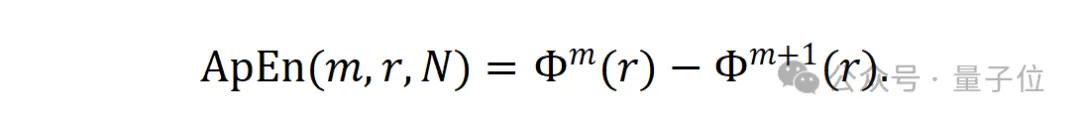
在后续对近似熵的计算中,研究人员将容差设定为r = 0 。这一决定是基于推荐物品的独特特性,其中具有相似ID的产品可能传达完全不同的意义。
总的来说,近似熵值越高,数据的重复率越高。
然而,传统熵通常与数据复制率呈现负相关性。因此,尽管ApEn被冠以”熵”的称谓,但其变化趋势与传统熵指标具有相反特性。
为避免概念混淆,本研究采用ApEn′=1/ApEn作为近似熵的最终测度。研究人员进一步引入数据平均最小编码长度作为最终的数据质量衡量指标。
由于重复的序列模式均可用相似的编码表征,从而降低平均最小编码长度,该指标将保障数据的最小可学知识量、有效防止重复与无效数据导致的数据量虚高问题。
研究证明了最小编码长度有如下的下界保障引理。
假设用户序列可以被建模为一阶非周期性平稳马尔可夫链。如果用户序列为S={S,∈U } ,那么所有序列的最小编码长度之和|U|L(C)由以下公式给出:
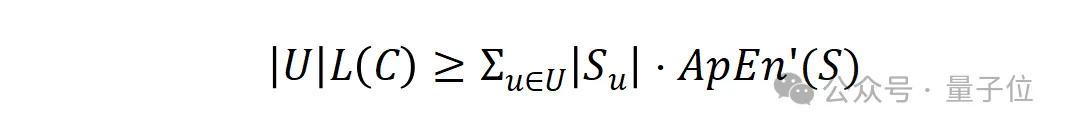
这个下界表达了在给定的用户序列情况下,最小编码长度应该至少等于序列元素长度总和除以序列的近似熵。这个不等式利用了近似熵的概念来提供编码效率的下界。
于是研究人员将D′=∑∈U|S| · ApEn′(S)代入了原有的扩展定律公式D。
研究人员进一步证明能将每一项参数用1/x+log(x)的形式以加入衰减项,从而优化性能拟合。他们拟合模型的最终形式为:
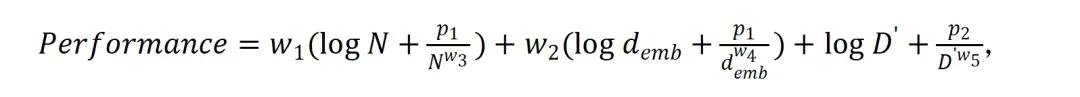
其中N为模型层数,demb为嵌入维度,D′=∑∈U|S| · ApEn′(S)为数据质量衡量指标,其余均为拟合参数。
实验环节
验证实验
研究人员的验证实验目标是验证理论的准确性,主要从两个方面进行:一是其模型是否符合扩展法则,二是使用近似熵(ApEn)和标记数量来评估数据规模的方式是否合适。
他们首先检查模型损失曲线与扩展法则的一致性,从图像上可看出实际模型性能非常贴合其表现定律。
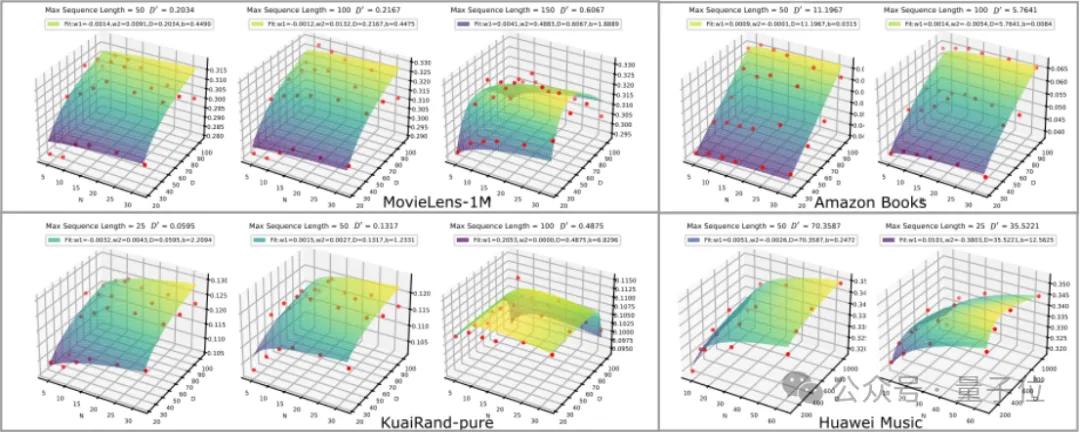
然后,数据参数D’加入参数进行一并拟合,以研究其影响因素。在下图中他们拟合的数据参数与ApEn的组合呈现出明确的线性关系,这证明了理论的有效性。
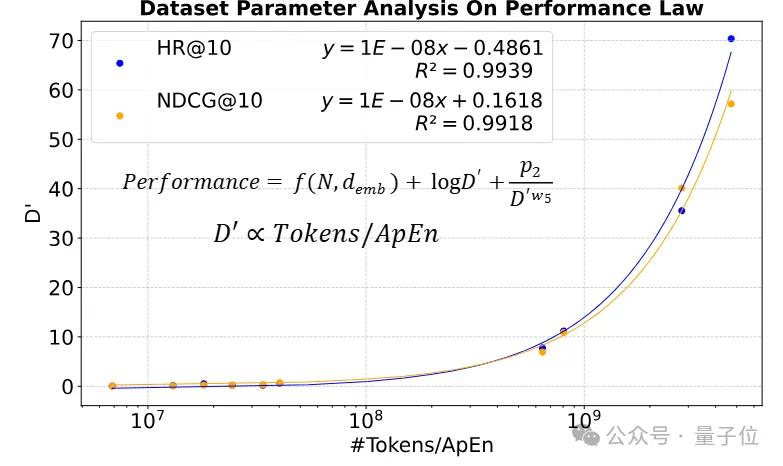
应用实验
由于性能法则中包含衰减项,使得实现全局最优解成为可能。
在前述拟合分析的基础上,研究人员在下表从全局和给定参数规模篇两个方面利用Performance Law给出了两个参数最优拟合,均获得了较好的结果。
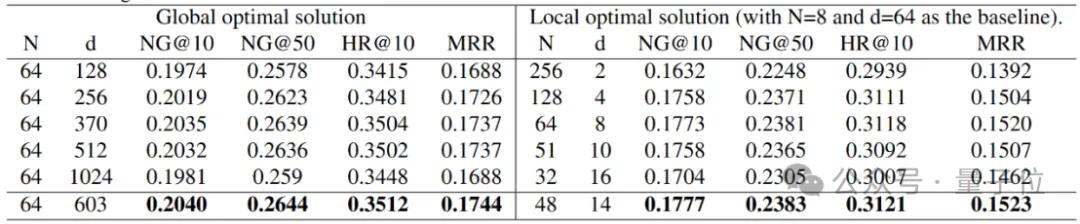
同时研究人员也可以在小规模实验上分析拟合参数对模型增大时的提升潜力与全局最优性能进行预测。
他们在下表验证了这个应用,在更小的衰减项参数上模型的扩展潜力更大,最优结果更强。

更多细节欢迎查阅原论文。
论文链接: https://arxiv.org/abs/2412.00430
- 百度AI搜索上线DeepSearch,支持主动思考和无限次免费使用2025-05-16
- 悠易科技战略升级:推出AI智能体矩阵,开启AI全域营销新征程2025-05-15
- 拿下38项第一!字节发布Seed1.5-VL多模态推理模型2025-05-14
- 6个月估值翻倍!黄仁勋力荐的AI搜索公司欲开发浏览器取代Chrome2025-05-13