Meta版慢思考来了！田渊栋团队整合快慢思考，能走迷宫推箱子
性能提高但推理成本更低
明敏 发自 凹非寺
量子位 | 公众号 QbitAI
Meta版慢思考也来了。
田渊栋团队带来新作Dualformer，把快慢思考无缝结合，性能提升还成本更低。
能解决迷宫、推箱子等复杂问题。
通过让模型在推理轨迹和最终答案上进行训练，再基于特定策略丢掉部分轨迹，Dualformer模型可以在模仿慢思考的同时，像快思考一样走捷径。
由此能形成更简洁的思维链（CoT）。
从结果来看，在慢思考模式下，Dualformer的最优解率达到97.6%，推理步骤减少45.5%。
自动切换快慢思考模式下，最优率也达到96.6%，且推理步骤减少59.9%。
搞定o1玩不来的迷宫游戏
o1带火了系统2（慢思考），能让大模型推理能力大幅提升。
但是随之而来的计算成本更高。
Dualformer能很好结合快慢思考，从而缓解这一问题。
它建立在Searchformer这项工作的基础上。Searchformer是一个可以解决复杂推理任务的模型，在A*搜索算法生成的路径上训练而来，在路径规划任务（如迷宫、推箱子游戏）上表现良好，可以以更高效率找到最优解。
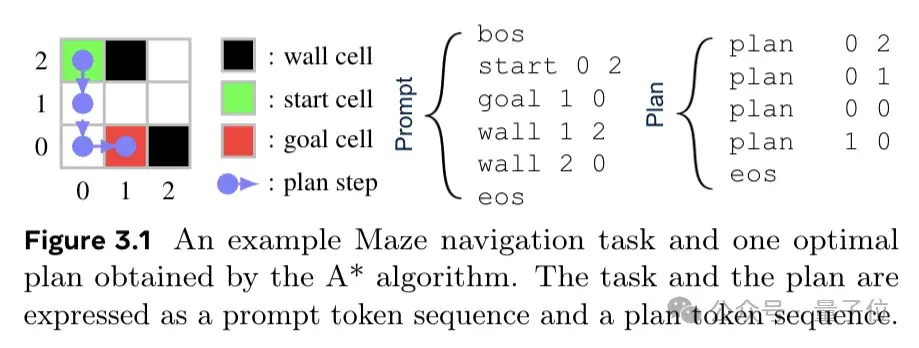
研究发现，人类会在思考过程中倾向于找捷径。为了更进一步模拟人类，Dualformer在随机推理轨迹数据上进行训练，并在训练过程中依据定制的丢弃策略丢到部分结构。
比如在处理路径规划任务时，根据搜索轨迹中的不同子句（如close子句、子句中的cost tokens、create子句等）设计了四个级别的丢弃策略，从只丢弃close子句到丢弃整个轨迹，并在训练时随机选择应用这些策略。
基于这些策略，Dualformer可以学习更简洁有效的搜索和推理过程。
在推理阶段，Dualformer可配置快速模式（仅输出解决方案）、慢速模式（输出推理链和最终解决方案）或自动模式（自行决定推理模式）。
这种灵活的推理模式设计使得模型能够根据不同任务需求和场景进行自适应调整，类似于人类思维在不同情况下的决策方式。
在具体任务上，研究设置了迷宫(Maze)和推箱子游戏(Sokoban)，让模型进行路径规划。以及数学推理任务。
对比来看，在迷宫任务中，o1-preview和o1-mini模型输出的路径并不好，会“穿墙”。
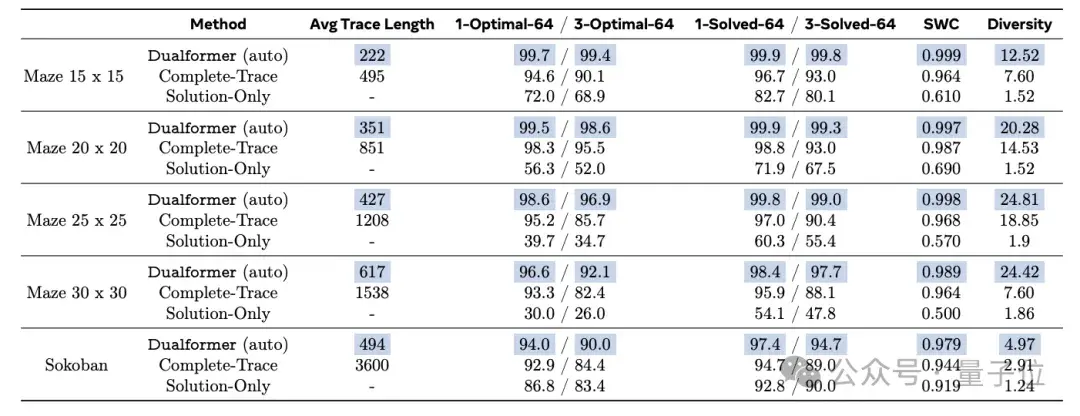
快思考模式下，Dualformer的表现如下。
Dualformer以80%的最优率完成这些任务，显著优于仅基于解决方案数据训练的Solution-Only模型，后者的最优率仅为 30%。
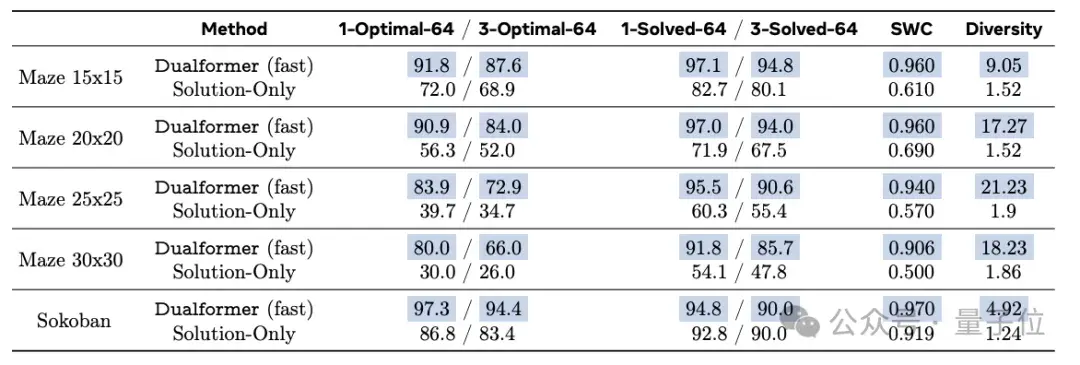
慢思考模式表现如下。
30×30迷宫任务中，在97.6%的情况下可以达到最优解，同时推理步骤减少45.5%。
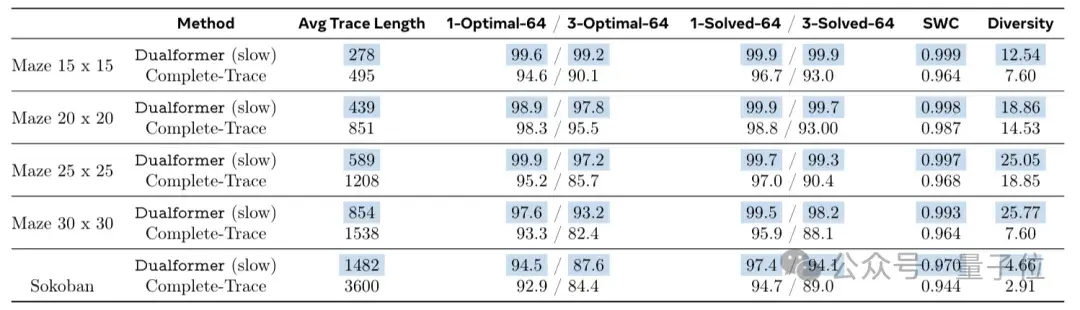
自动切换快慢思考模式下，Dualformer的最优率达到 96.6%，与Searchformer相比，推理步骤减少59.9%。
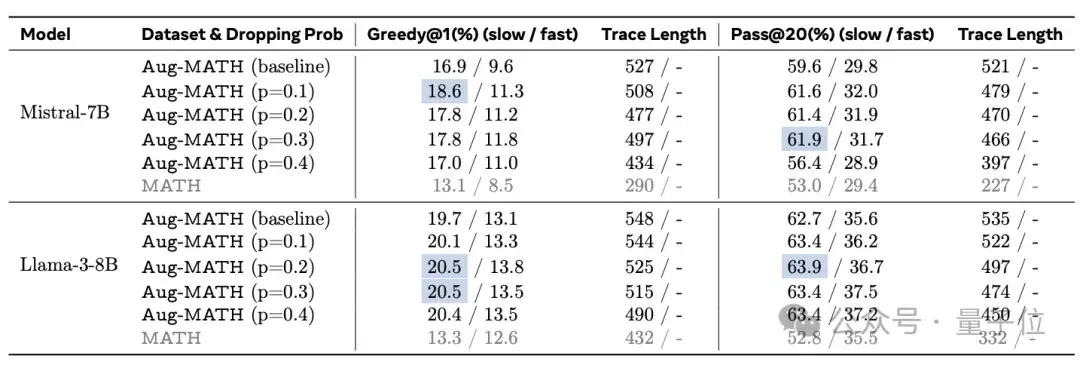
将该方法推广到Mistral-7B和Llama3-8B上，在Aug-MATH数据集上，模型的表现都有所提升。
比如在Mistral-7B模型上，当p=0.1、0.2和0.3时，Pass@20度量的基线模型，其中绝对正确率增加到61.9%。
最后，来看一下研究团队阵容。
该研究由田渊栋等人带来。
田渊栋现在是Meta FAIR的研究科学家主任，领导LLM推理、规划和决策小组。
Qinqing Zheng是FAIR的工程师，研究方向集中在生成模型和强化学习方面。她本科毕业于浙江大学，在芝加哥大学攻读博士学位。2017-2019年期间在Facebook担任研究科学家，帮助Facebook建立了广告推荐模型的分布式训练系统。
Sainbayar Sukhbaatar是FAIR的研究科学家，主要负责大模型推理和记忆方面研究。他曾先后在谷歌、DeepMind、Meta任职。
Michael Rabbat是FAIR的创始成员之一。加入Meta之前他曾是麦吉尔大学计算机工程系教授。研究领域包括机器学习、分布式算法、信号处理等。
论文地址：
https://arxiv.org/pdf/2410.09918
- 最强开源CodeLLM模型深夜来袭！320亿参数，Qwen2.5-Coder新模型超越GPT-4o2024-11-12
- ¥9.99租英伟达H800！双十一算力羊毛真香，闲置卡也能挂机变现2024-11-04
- 最高精度1公里*1公里*1小时！达摩院发布气象大模型，落地大山东2024-11-07
- 时代变了！英伟达纳入道琼斯指数，英特尔被取代2024-11-02
相关阅读
