矩阵乘法无需相乘,速度提升100倍,MIT开源最新近似算法 | ICML 2021
无需“乘加”操作
萧箫 发自 凹非寺
量子位 报道 | 公众号 QbitAI
在不做乘加操作(multiply-adds)的情况下,能计算矩阵乘法吗?
矩阵乘法包含大量a+b×c类运算,因此常在运算中将乘法器和加法器进行结合成一个计算单元,进行乘法累加操作。
用近似算法的话,确实可以!
这是来自MIT的最新研究,他们提出了一种新的近似算法MADDNESS,在确保一定精度的情况下,将速度提升到了现有近似算法的10倍,比精确算法速度快100倍,被ICML 2021收录。

研究还认为,新算法可能比最近大火的稀疏化、因子化等操作更有前途。
目前,作者已经开源了算法代码,感兴趣的小伙伴们可以去尝试一下。
一起来看看。
用K聚类算法搞个查找表
这个算法,借鉴了一种叫做乘积量化(Product Quantization)的方法。
其中,量化本质上是一种近似操作。
由于矩阵乘法中的每个元素,都可以看做是两个向量的点积,因此可以通过查找相似向量,来近似地估计向量的点积,而无需再进行大量乘法运算。
乘积量化的具体原理如下:

当我们输入一个要计算的向量a的时候,函数g(·)会对a进行一个近似操作,从一个提前设置好的数值查找表中,找到与它最相近的那个值,并输出一个近似的向量g(a)。
与此同时,这张表格中的每个值,都已经提前做过点积计算了,因此在输出g(a)的同时,它与查询向量(query vector)b对应的近似点积计算结果h(b)也能被查表并输出。
最后,只需要用f(·,·)函数对g(a)和h(b)做加法运算,而不需要再做乘法计算了。
简单来说,就是通过近似查表的方法,节省了矩阵乘法中的乘法计算时间。
那么,这样的数值查找表,究竟要设置什么数值,才能确保在近似计算过程中,损失的计算精度最小呢?
这里借鉴了一下K聚类算法(K-means)的思路,即将数据预分为K组,随机选取K个对象作为初始聚类中心,再通过训练迭代,确保在将样本分到K个类中时,每个样本与其所属类中心的距离之和最小。

△可视化的K聚类算法
通过这种方法计算出来的数值查找表,能更准确地近似矩阵乘法的数值计算结果。
根据这样的思路,作者们提出了一种高效的向量乘积量化函数,能在单CPU中每秒编码超过100GB的数据;同时,还提出了一种针对低位宽整数的高速求和函数。
然后,基于这两类函数,整出了一套全新的矩阵乘法算法MADDNESS。
这个近似算法的效果如何呢?
精度保持,效率提升数倍
这个算法所需要的算力并不高,在搭载英特尔酷睿i7-4960HQ(2.6GHz)处理器的Macbook Pro上就能完成。
他们在Keras版本的VGG16模型上进行了测试,所用的数据集是CIFAR-10/100,对一系列最新的近似算法进行了评估:
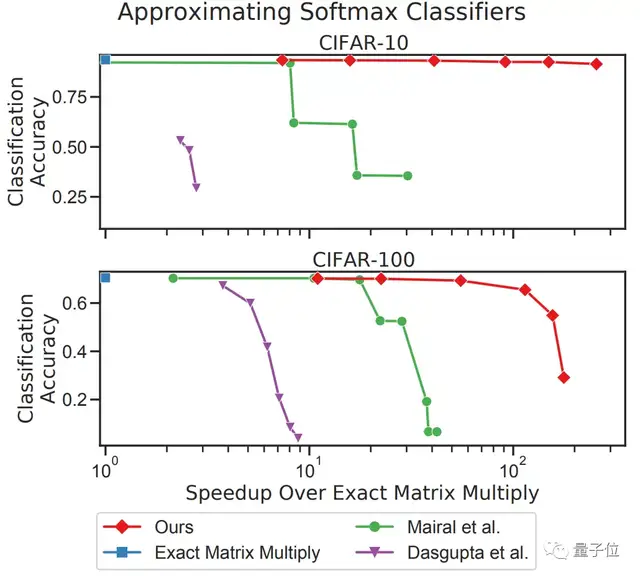
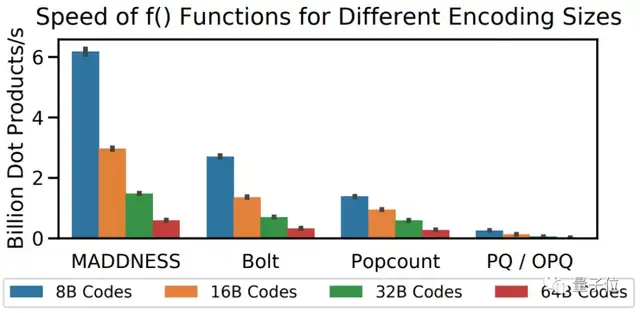
从图中来看,在效率提升接近10倍的情况下,采用MADDNESS(图中红线)仍然能在CIFAR-10上保持几乎不变的精度。
即使是在CIFAR-100上,在精度几乎不变的情况下,MADDNESS和MADDNESS-PQ也同样实现了效率最大化的结果。
除了最新算法外,与其他的现有算法相比(包括作者们在2017年提出的Bolt算法),效果同样非常拔尖。

对比计算速度的话,MADDNESS的点积速度就能比现有最快方法快两倍左右。
当然,也有读者指出,这篇论文还存在一些待解决的问题:
①论文用的是VGG16模型,但没有在Transformer等更经典的模型(如BERT)中进行实验;②虽然对矩阵乘法进行了加速,但毕竟只是近似算法,意味着潜在的精度损失;③没有在GPU中测试评估结果。

但他仍然认为,这不失为一篇非常有意思的研究。
作者介绍

Davis Blalock,MIT的计算机系博士生,致力于研发快速机器学习算法,他认为速度是衡量机器学习模型的一个非常重要的因素。

John Guttag,MIT计算机系教授,研究方向是机器学习、AI和计算机视觉,目前的研究项目集中在医疗AI和医学成像上。
值得一提的是,这两位研究人员,此前还炮轰过神经网络中的剪枝算法。

他们针对其中的81种算法进行了横向对比,发现“没有明确证据表明,这些算法在10年内,对任务效果有明显改善”。
研究一作Davis Blalock还认为:
这些改进都是所谓的“微调”,而不是科研人员声称的“核心创新”,甚至有些改进方法可能根本就不存在。
在对AI模型进行效率提升上,两位作者确实是很严格了。
项目地址:
https://github.com/dblalock/bolt
论文地址:
https://arxiv.org/abs/2106.10860
参考链接:
[1]https://mp.weixin.qq.com/s/VK2W9zD83ddSzYSLLS21UQ
[2]https://news.ycombinator.com/item?id=28375096
- 首个GPT-4驱动的人形机器人!无需编程+零样本学习,还可根据口头反馈调整行为2023-12-13
- IDC霍锦洁:AI PC将颠覆性变革PC产业2023-12-08
- AI视觉字谜爆火!梦露转180°秒变爱因斯坦,英伟达高级AI科学家:近期最酷的扩散模型2023-12-03
- 苹果大模型最大动作:开源M芯专用ML框架,能跑70亿大模型2023-12-07