潘建伟团队再次展示量子计算优越性！“祖冲之号”1.2小时就能完成超算8年计算量
距“九章”只过了7个月
明敏 梦晨 发自 凹非寺
量子位 报道 | 公众号 QbitAI
潘建伟团队宣称又一次实现了“量子计算优越性”！
世界最强的超级计算机8年才能完成的任务，用“祖冲之号”量子计算机最短1.2个小时就能实现。
这距离我国2020年12月4日首次实现量子计算优越性，仅仅过去了7个月。
这项工作由潘建伟、朱晓波、彭承志带队完成，相关论文预印版已上传至arXiv上。
这次的“祖冲之号”与当年谷歌宣称实现量子霸权的Sycamore量子计算机，都采用了超导量子计算。
这是目前最有希望实现可拓展量子计算的候选者之一。
其核心目标是如何同步地增加所集成的量子比特数目以及提升超导量子比特性能，从而能够高精度相干操控更多的量子比特，实现对特定问题处理速度上的指数加速。
总而言之就是一个字——快。
“祖冲之号”使用56个量子比特，就比Google Sycamore量子计算机53个量子比特强2~3个数量级的量子优越性。
所以论文以“Strong quantum computational advantage”为题，代表更能证明量子计算的优越性。
此外，此次“祖冲之号”可以称得上是2.0版本，在量子相干时间等方面都有了很大的提升。
祖冲之号
祖冲之号于今年5月刚刚研制成功，并在此基础上实现编程的二维量子行走，论文发表在当月Nature上。
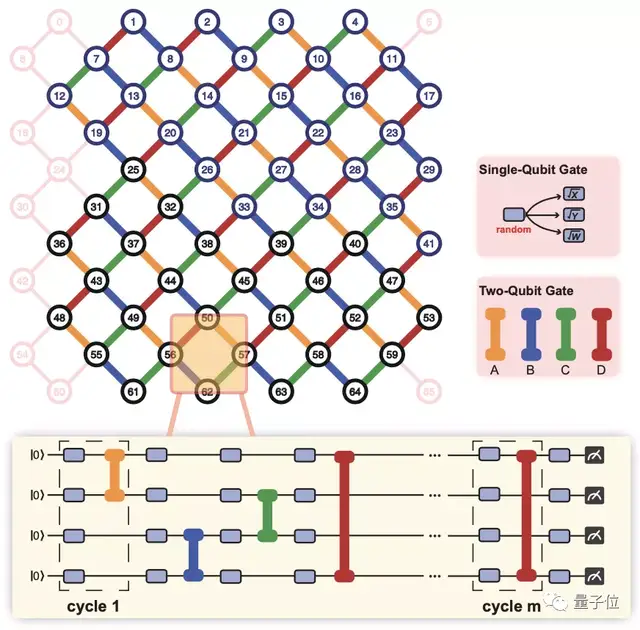
这次祖冲之号所用的量子处理器由66个Transmon量子比特组成，比5月刚研制成功时又增加了4个。
这些量子比特排列成11*6的晶格。
Transmon本质上是一种非线性振荡器，其非线性来源于超导约瑟夫效应。非线性振荡器的最低两个能级被挑出来，就形成一个量子比特。
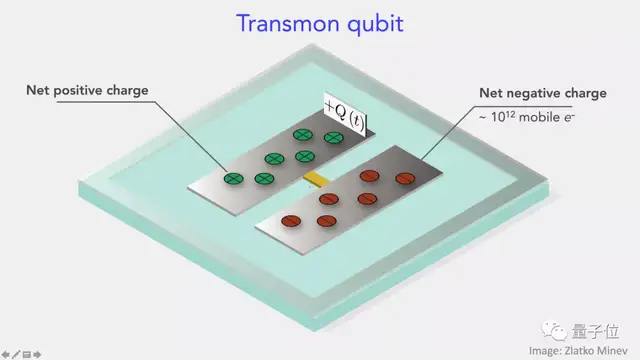
两个量子比特之间由一个频率更高的Transmon连接作为耦合器，可以快速调整相邻的量子比特之间的耦合强度。
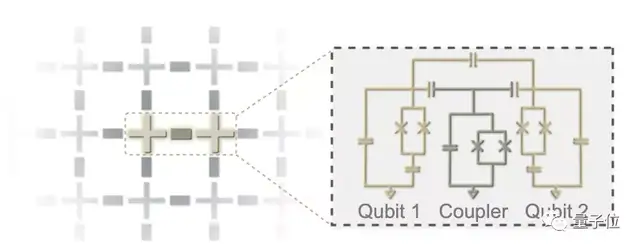
这样的量子处理器的实现了高保真的单量子比特门（保真度平均99.86%）和双量子比特门（平均99.41%），以及95.48%的读出。
为了验证量子处理器的性能，团队选取了其中的56个量子比特进行20个周期的随机量子电路采样任务，创造了挑战经典计算机的新纪录。
量子计算全球竞争激烈
值得一提的是，在中科大发布此次成果后的第二天，IBM也宣布了在量子领域的下一步计划。
他们宣布，将在2023年之前建立一个有1211个量子比特的系统；未来将向100万以上量子比特的系统发起挑战。
全球量子计算领域的激烈竞争，可见一斑。
2019年，谷歌最早宣布实现“量子霸权”。
他们宣称，利用Sycamore量子计算机的53个量子比特，可以在200秒内处理世界超算1万年才能完成的任务。
不过这一结论很快遭到了IBM研究人员的质疑，并在arXiv上刊出了他们的成果。
IBM在文章中指出，利用他们的方法，经典超级计算机可以在2.5天内以更高的保真度完成相同的计算任务。
2020年12月4日，中国科学技术大学发布使用76个光子的量子计算机“九章”，并宣布实现量子优越性。
由此，我国成为全球第二个实现“量子优越性”的国家。
不过，“九章”量子计算机目前还不能通用于玻色采样以外的其他计算，不具备通用性。“祖冲之号”所应用的超导量子计算更有希望在实际中应用。
近年来，谷歌、IBM等公司纷纷对外宣称成功开发出了大数量（50以上）量子比特的量子计算原型机。
但实现量子计算的关键参数不仅仅是量子比特数量，还有系统的保真度。
随着量子比特数量和循环次数的增加，保真度都会急剧下降，错误率会相应上升。
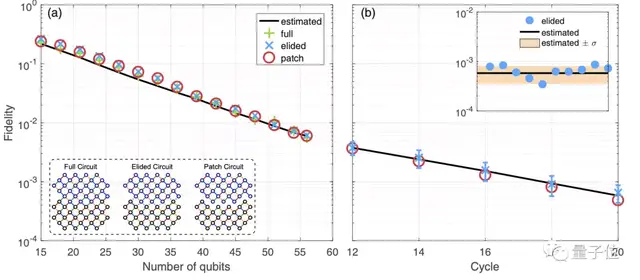
因此，量子计算机距离走向实际应用，目前还比较遥远。
值得一提的是，就在最近潘建伟团队还有另一项研究成果发表。
研究出了迄今为止最快的实时量子随机数发生器（QRNG），速度达18.8Gb。
其尺寸只有15.6×18.0毫米，远远小于大多数QNRG模块或仪器。
目前，这项成果已发表在《应用物理快报》上。
本次论文：
https://arxiv.org/abs/2106.14734
祖冲之号论文：
https://science.sciencemag.org/content/372/6545/948
参考链接：
[1]http://news.ustc.edu.cn/info/1048/75066.htm
[2]https://twitter.com/zlatko_minev/status/1287217387947925504
- 开源Llama版o1来了，3B小模型反超80B，逆向工程复现OpenAI新Scaling Law2024-12-17
- AI音乐战火升级！三路国产大军全面对决Suno2024-12-11
- o1满血版最鲜测！这¥1500花得值吗？2024-12-06
- 谷歌邀马斯克联手做AI游戏！DeepMind版Sora是个3D游戏引擎 profile-avatar2024-12-05
相关阅读
