三体人有救了，只要等得够久就会有一个太阳被甩出去

梦晨 萧箫 发自 凹非寺
量子位 报道 | 公众号 QbitAI

刘慈欣的科幻小说《三体》，让很多人知道了“三体问题”这一世纪难题。

这个问题，最初由牛顿提出。

当时，在用万有引力定律解释了行星(如地球)如何绕太阳运动的“二体问题”后，牛顿又想到了一个进阶问题：

在太阳和地球的双重影响下，月球如何绕地球运动？

于是，他在《自然哲学的数学原理》中提出了三体问题：

三个可以视为质点的天体，在其相互之间的万有引力作用下，应该如何运动？

牛顿的经典力学，描述了一个决定论的世界。拉普拉斯曾断言：“只要知道宇宙中所有粒子的当前位置和速度，原则上就有可能预测任何时刻的情况。”

本以为只是二体问题之上再加一个体而已，很快就能解决。

没想到，牛顿根本找不到这个问题的通用解！

几代科学家经过努力，也只找出三体问题在一些限制条件下的特殊解。

例如位于非等边三角形顶点的三个等质量质点，在初速度为0时的运动规律，几乎毫无章法。

牛顿之后，欧拉、拉格朗日、泊松等许多数学家都向三体问题发出挑战，但依然找不出它的通用解。

三体问题难在哪里？

其实，早期的科学家根本没有意识到，他们试图解决的三体问题难度有多么恐怖。

直到1885年，瑞典数学杂志Acta Mathematica举办了一次国际数学大赛，其中第一道题是比三体问题还难的N体问题。

对于一个根据牛顿定律相互吸引的多质点系统，假设没有两点发生过碰撞，请找出各点坐标在已知时间函数中的序列展开，在任意时间段内均匀收敛。

翻译一下就是：太阳系稳定吗？会把我们的地球甩出去吗？

时年29岁的法国数学家庞加莱接受了这一挑战。二体问题此前已被牛顿解决，于是庞加莱从限定条件下的三体问题入手：

假设其中两个质点的质量足够大，使得第三个质点的质量对前两个不造成影响（有点像是研究两个行星和一粒灰尘之间的相互作用）。

这还不够，再把它们的运动都限制在同一个平面上。

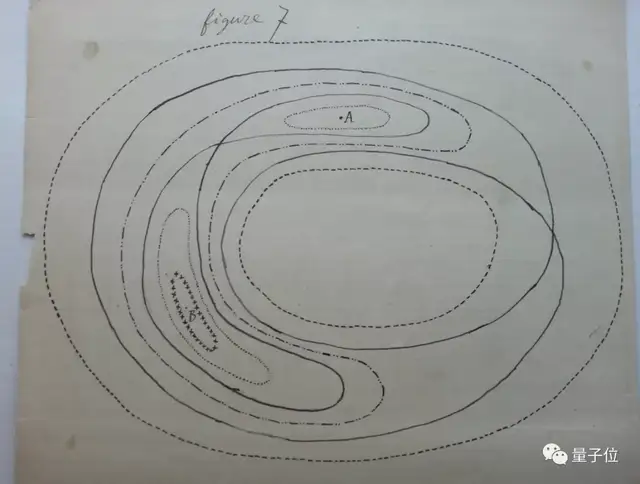
△庞加莱手稿

怎么样，够简化了吧。

可是庞加莱用了整整三年时间也没得出完整结果，只是解出了一些特殊情况。最后赶在大赛截止日期前提交了论文，还成功胜出，领到了奖金，美滋滋。

△庞加莱

然而在论文出版之前，审稿人对论文的某一部分看不太明白，写信向庞加莱请教。

庞加莱细化自己的论证时，却发现了致命错误，赶紧联系出版社撤回已经印刷的论文，又把奖金全赔进去了。

在修订论文的过程中，庞加莱发现了三体系统对初始条件的敏感依赖性。

即使完全知道了运动的规律，初始条件的细微差别，有时也会造成系统随后运动的极大不同，使长期预测变得不可能。

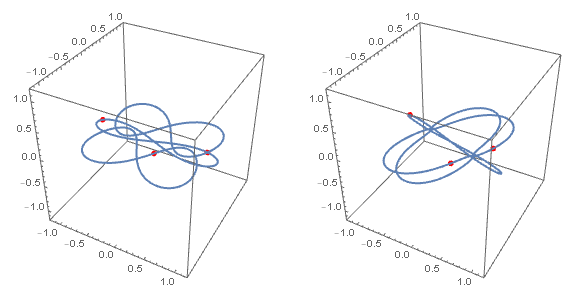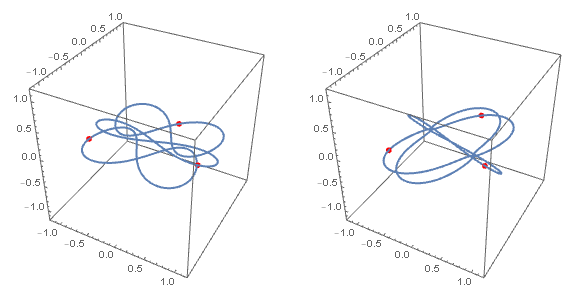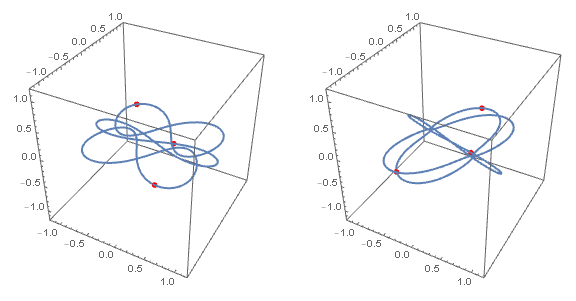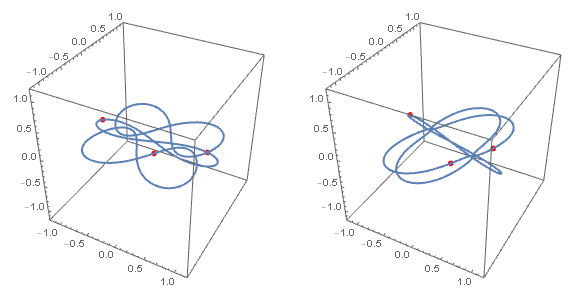
这个现象后来被称为混沌。

这就是《三体》小说中三体人面临的生存难题了——

在那个世界中，太阳有3个。

由于三个太阳运动轨迹的混沌性，三体人会遭遇昼夜季节无规律更替的“乱纪元”，极端天气带来严苛的生存环境让三体文明不断地毁灭。

现实地球上的天气变化虽然没那么危险，但也是混沌系统。

气象学家洛伦兹用“蝴蝶效应”来解释这种现象，即蝴蝶扇动翅膀造成初始条件的微小差异，经过时间的放大都会造成剧烈的变化。

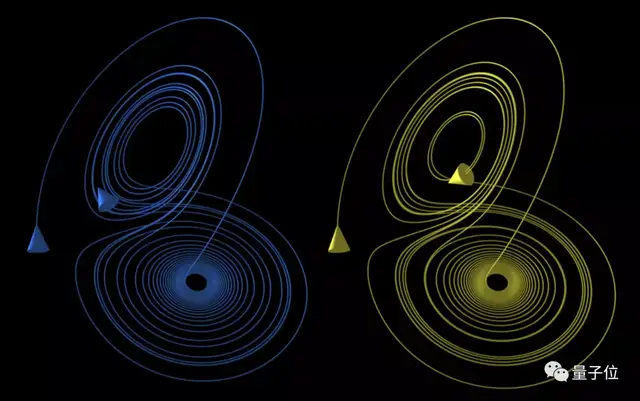
后来，有了计算机的帮助，科学家们能够计算出更多三体问题中，一些存在周期性的特殊解。

如2017年，来自上海交大的研究团队就利用超级计算机，一口气发现了600多个全新的周期解。

但三体问题的通用解，还笼罩在混沌的阴影下。

这次做出了什么突破？

既然是混沌系统，那就没办法了。

但并不意味着“三体系统”就研究不了——

这不，还有统计学嘛。

统计力学的著名科学家路德维希·玻尔兹曼，在1871年曾经提出过一个假说：

各态历经假说(ergodic hypothesis)：一个孤立系统从任一初态出发，经过足够长的时间后，将经历一切可能的微观状态。

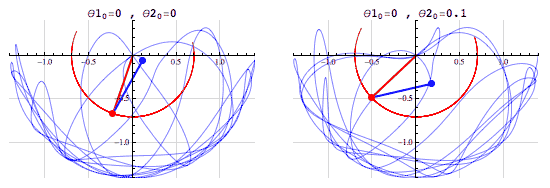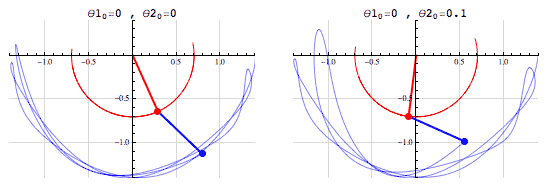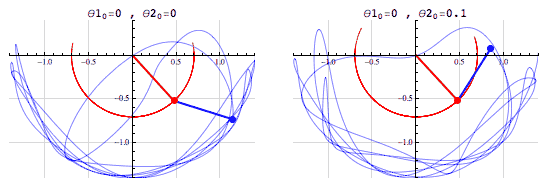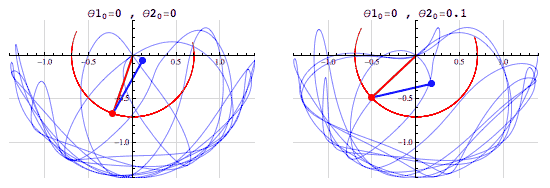
△双摆系统，混沌系统之一

孤立系统，从热力学角度来说，指不与外界交换能量或质量的系统。

只要时间够长，这种系统中所有可能的状态都会发生。

在这个前提下，加上计算机和计算物理学的发展，苏联科学家在20世纪60年代有了新的突破。

对于由质量无等级差距的三个物体形成的“非层级三体系统”，有一个状态是最可能发生的——

其中一个体最终会逃逸出去，另外两个演变成规律运动、可预测的“双星”系统。这个过程被称作三体系统的衰变(Decay)。

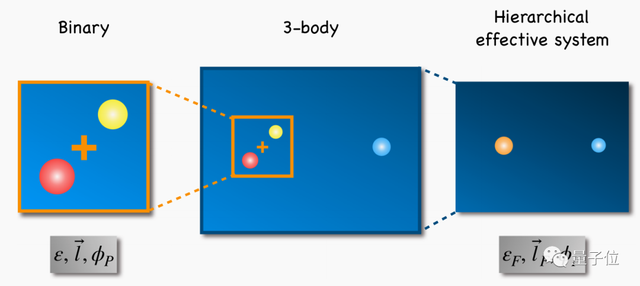
△就像这样

不禁让人想到这个场景……（手动狗头）

就这样，研究的目标变成了“三体问题的统计预测是怎样的”。

之后的研究发展并完善了使用相空间(Phase Space)来描述三体系统状态的方法。(相空间是一个假想的空间，系统每个可能的状态都对应相空间中的一个点)

时间来到2019年，来自希伯来大学的Nicholas Stone等人，终于在此基础上得出了非层级三体问题的统计学闭合解。

然而，这项研究还有一些瑕疵。

按照牛顿的理论，引力是无距离限制的。导致描述三体系统状态的相空间的体积也是无限的。

Stone团队人为假设了一个“强相互作用区域”来解决这个问题。

还有，用相空间体积来确定概率，从而忽略了相空间的相当一部分区域描述的是有规律、可预测的运动情况，其中包括系统衰变后剩下二体的运动。

△特定初始条件下的规则运动

同样来自希伯来大学的物理教授Barak Kol，将研究对象聚焦在系统衰变时相空间的流出通量(Outgoing Flux)上，而不是相空间本身。

这样即使相空间是无限的，其通量也是有限的，就无需引入假设的强相互作用区域了。

Kol团队还补充了统计演化模型来计算系统衰变，可以呈现为下面这张管道图。

从图中来看，三体系统的运动状态可以分成两种，规则(regular)和遍历(ergodic)，其中遍历的情况要明显多于前者。

而逃逸的情况，也同样分成两种，逃逸(escape)和偏移(sub-escape)。

Kol团队把三体系统的状态变化类比成在一个有光滑反射壁和一个小孔的瓶子里不断反射。

在经过一段时间后，从小孔脱离遍历的系统状态会进入“逃逸”或是“偏移”。

用这种统计方法预测的质点逃逸概率，比2019年和2006年的两项研究所做的统计预测，都要更接近数值模拟值。

下图是三个“三体”星系的质量，以及它们逃逸的概率预测(其中M☉是太阳质量，约为2×10³º千克)。

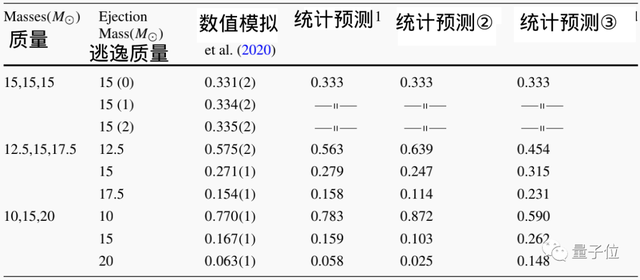
其中，“统计预测1”是这次研究的预测结果。

从图中可见，相比于其他两项最新研究，这一研究的统计预测结果，都更加贴合用“数值模拟”计算所得到的质点逃逸率。

当然，从图中也能看出，质量更小的质点更容易发生“逃逸”情况。

对于这项研究给出的统计方法，论文作者、物理教授Barak Kol表示：

在数百万台计算机上进行的模拟测试表明，这一理论所计算的结果，和计算机模拟的结果高度符合。

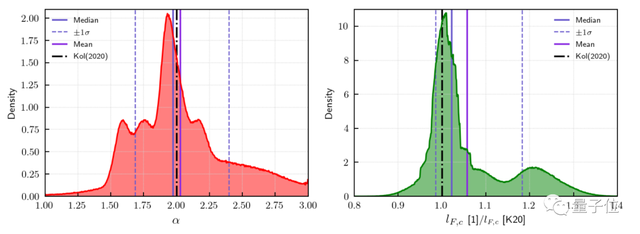
希伯来大学出品

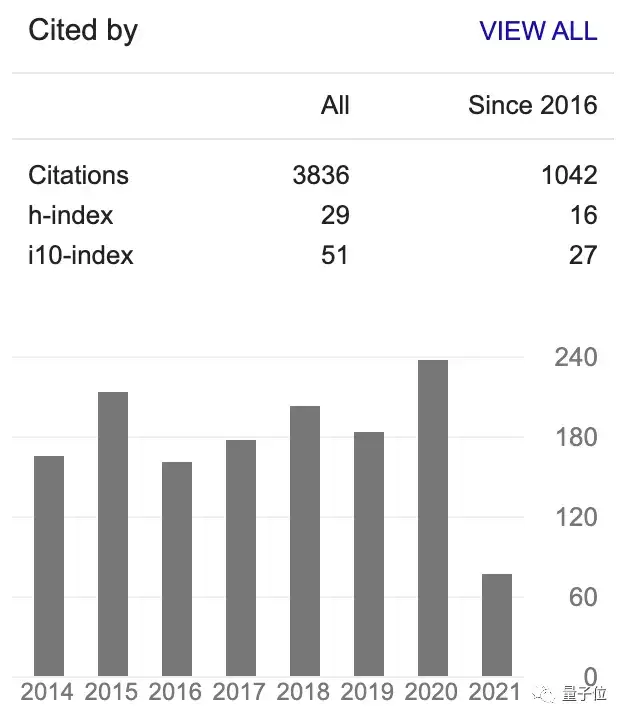
这次的论文作者Barak Kol，是以色列希伯来大学的一名物理教授，曾于斯坦福大学获得物理博士学位，还在特拉维夫大学、普林斯顿大学从事过博士后工作。

PS，如果想要自己制作“三体”模拟动画的话，还可以用文末的Universal Sandbox游戏试试~

可在任意位置添加天体，并修改质量、体积等属性，然后观察运动轨迹。

论文地址：
https://link.springer.com/article/10.1007/s10569-021-10015-x

上海交大600个三体特殊解动画：
http://numericaltank.sjtu.edu.cn/three-body/three-body-movies.htm

Universal Sandbox：
https://store.steampowered.com/app/230290/Universe_Sandbox/

参考链接：
[1]http://www.mittag-leffler.se/library/henri-poincare
[2]https://mathematica.stackexchange.com/questions/135857/jacobian-of-parametricndsolve-and-findroot-for-the-three-body-problem
[3]https://phys.org/news/2021-y-theory-centuries-old-physics-problem.html
[4]https://nature.com/articles/s41586-019-1833-8
[5]https://arxiv.org/abs/2101.03661

— 完 —