妙哉!那个用文言文编程的小哥,竟从28万行唐诗中找出了对称矩阵
只找出2个
梦晨 萧箫 发自 凹非寺
量子位 报道 | 公众号 QbitAI
你能看出来,这首诗妙在哪里吗?
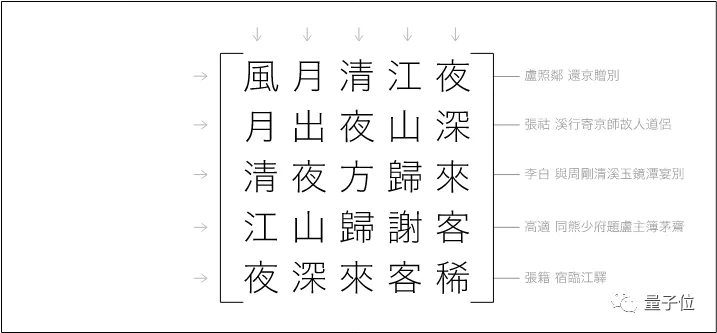
其实,横着读是一首诗,竖着读还是这首诗!
而且,这首诗可不是乱编的,其中的诗句都来自《全唐诗》,读起来也颇有意境。
创造这个奇妙组合的,不是文学研究大师,而是一位程序员小哥。
他用计算机,找出了所有符合规律的古诗,还在Github上开源了代码。
就连README文件,也颇具个性:
余所用之程序,當以gcc編譯之如是
gcc -O3 mgsq5.c -o mgsq5
等一下。这个风格好像很熟悉?
没错,这位程序员,正是之前开发了火遍全网的文言文编程语言的Huang Lingdong。
△ 文言文编程的“Hello,World”
他用数学中的3阶幻方(九宫格)作比,把符合这种规律的诗命名为“唐诗幻方”。
然而,这首诗真正的玄妙之处,还不止在这里。
玄妙之处
这首诗,初看只是横竖都能读,但如果把其中汉字编码成数字再看的话,会发现:
原来,这是个对称矩阵!
不过,他遍历了全唐诗里所有五言诗共二十八万七千句后,也只能得出两个这样的幻方。
除了“风月清江夜”以外,还只有一个,不过意境上差了许多,不能令他满意。
在135600行七言唐诗中,符合这个规律的七言“幻方”,更是一个都没有。
他只能退而求其次,只寻找奇数项对称的,即每句第1、3、5、7个字对称,偶数行用空行代替。
放宽标准后倒是能找出不少,但再想从其中挑选符合音韵格律、意思上还通顺的,就不多了。
最后,他选择了其中一个还稍微过得去的做例子,把空行中的字也加上,也能写成对称矩阵:
这位小哥,是在研究传统文化时,从古代的洛书和璇玑图中获得的灵感。
△洛书
洛书写成数字就是三阶幻方,特点是每一行、每一列及对角线中的数字之和都相等。
文字没有求和这种操作,如果按照程序员思维,那就是字符串拼接起来相等。
就这样,得出了要寻找的目标:第n行和第n列的文字相同。
璇玑图中共841个字,按顺读、逆读、横读、斜读、蛇行读、交叉读、换行读、换列读、间句读都能成诗,总共包含了7958首诗。
其中的关键之处在于,按照不同顺序读,其文字都能组成有意义的诗句。他自认没有古人作诗的才华,就想到从唐诗中寻找符合条件的诗句。
而且是用现代人的方法——编程来解决。
以“暴力”治之
这位小哥,先是想到了用“八皇后问题”的计算机解法,来找出符合要求的唐诗。
八皇后问题,简单来说是这样的:
8×8的国际象棋棋盘上,摆放8个不同的皇后,使其不能互相攻击,即处在同一行、同一列、同一斜线上,求解摆放方法。
这个问题,可以用到一种名为“回溯法”的算法来求解,原理如图:
如果用回溯法来找“幻方”,计算机需要先随机“找出半句诗”,再挨个儿往后面搜索合适的诗句。
例如,计算机先从13万行唐诗中,随机找出诗句“风月清江夜”:
根据对称矩阵的原理,第二句诗的开头,就应该以“月”为首:
(以月开头的诗句,应该还是有不少的,像月上柳梢头)
以此类推,第三句诗的开头,就应该以“清夜”为首:
(以清夜开头的诗句,就少了许多)
而第四句诗的开头,就应该以“江山归”打头:
(江山归开头的诗……可选范围应该更少了)
最后一句诗的开头,就必须与前4句诗的结尾完全一致,“夜深来客”:
难度逐渐变成地狱级……
在这几步操作中,要是有任何一步无法满足条件,就得全部推倒重来。
这样的话,最初的第一步,就显得尤为重要:从什么类型的诗句开始遍历,才能最快地找到答案?
他为此用上了启发式搜索,从已知问题信息入手,对这些空格进行评估,找到限制条件最多、即最容易“下笔”的那个位置,再从这个位置开始找诗。
具体写成代码求解的话,就是利用递归法的结构。
同时,用上剪枝法,缩小剩下位置的查找范围。
也就是说,要用到约束函数,在扩展节点处剪去不满足约束条件的子树;再用限界函数,剪去得不到最优解的子树。
这样一来,就能降低问题复杂度。
然而在运行代码时,作者却发现,这样做效率并不高。
这种方法,虽然可以求解“N”皇后问题,却不太适合求汉字矩阵。
因为,要填进格子里的,可不止8个皇后,每一格可以填的汉字,就有5000+种选择!
采用递归法的话,计算机在填上前面的汉字时,实际上就缩小了剩下汉字可以搜查的范围。
如果没有找到最初那个合适的字,往往搜到一半后,能用的诗句就没了,又得重新再猜,效率不升反降。
越想越烦躁,这位小哥干脆一拍大腿:不如暴力搜索!
当然,也不是普通的暴力搜索。
会有两个搜索条件:
其一,以五言诗为例,第五列的前4个字,和第五行的前4个字,内容是否完全一样?如果不一样,就扔掉。
△ 第五行和第五列的前4个字
其二,这首诗是不是对称矩阵?不是的话,就扔掉。
利用C语言写好后,不用1小时就能跑出所有的“对称诗”。
作者表示,自己并非文学研究的专家,也不是算法专家,因此,这种方法可能并不是最好的办法。
诸君若有更好的求解思路,可以来找他玩耍~
作者介绍
作者Huang Lingdong,在发布文言文编程语言时还在卡耐基梅隆大学上本科。现在已毕业,在母校的Studio for Creative Inquiry做研究助理,为博物馆和学校等组织开发交互媒体项目。
这位小哥热爱编程和传统文化,还开发过写诗IDE,能自动检查平仄等格律规则,内置韵书和康熙字典做参考。
还能通过机器学习分析用户作品,并与《全唐诗》中的诗句做比对,看你写的诗像哪位诗人的风格。
除了诗词古文,他对传统美术也颇有研究,开发过无限生成随机山水画的工具,和多款中文字体。
△就是不知道为什么山水画里有个电线杆
项目地址:
https://github.com/LingDong-/magic-square-poems
Huang Lingdong主页:
https://lingdong.works/
- 首个GPT-4驱动的人形机器人!无需编程+零样本学习,还可根据口头反馈调整行为2023-12-13
- IDC霍锦洁:AI PC将颠覆性变革PC产业2023-12-08
- AI视觉字谜爆火!梦露转180°秒变爱因斯坦,英伟达高级AI科学家:近期最酷的扩散模型2023-12-03
- 苹果大模型最大动作:开源M芯专用ML框架,能跑70亿大模型2023-12-07